-
LCS (Longest Common Subsequence) 최장 공통 부분 수열💻 프로그래밍/알고리즘 2019. 6. 23. 16:42
안녕하세요! 코딩하는 JAY입니다. 오늘은 오랜만에 알고리즘 포스팅을 하려고 합니다:D
오늘 포스팅할 내용은 LCS, 최장 공통 부분 수열입니다.
주의해야할 점은 LCS가 두개라는 점입니다.
1. 최장 공통 부분 수열 = Longest Common Subsequence
2. 최장 공통 부분 문자열 = Longest Common Substring
이 두개의 차이저을 아래 예시로 말씀드리겠습니다.
1. ABCD, ABZC = AB
2. ABCD, ABZC = ABC
1번과 2번 예시의 차이점을 아시겠나요? 아마 차이점을 바로 눈치채셨을것 같아요 ㅋㅋㅋ
1번은 두개의 문자열을 비교했을때, 연속적인 문자열을 추출합니다.
2번은 공통된 부분 수열을 추출합니다(연속X)
여기서 핵심은 연속이냐? 아니냐 입니다 ㅎㅎ
최장 공통 부분 수열을 알아보기 전, 최장 공통 부분 문자열 즉, Logest Common Substring 에 대해 먼저 알아 보겠습니다!
1. Logest Common Substring
최장 공통 문자열의 핵심은 연속적이어야 한다는 것 입니다. 그림으로 먼저 확인해 보겠습니다.

위 이미지에서 가로줄을 x, 세로줄을 y로 보았을때, 문자열(jaycj)[x] 와 문자열(jay)[y]가 같을 경우 숫자가 1증가 합니다.
j = 1, a = 2, y = 3 이죠? 점화식으로 확인해보겠습니다.

앞에서 말씀드렸듯이 최장 공통 문자열은 연속적 이어야 합니다. 그래서 현재 위치와 비교하여 같은게 있을경우 x-1, y-1 바로 이전의 위치에 같은 문자가 있는 경우를 체크해 이전 값에 +1 하여 증가하게 됩니다. 같지 않다면 0! 이제 코드로 최장 공통 문자열의 길이를 구해보겠습니다.
12345678910111213141516171819202122232425262728293031323334def lcs_substring(n_list, input_name):for compare_name in n_list:LCS = [[0]*(len(compare_name)+1) for i in range(len(input_name)+1)]ans = 0pos = 0for i in range(1, len(input_name) + 1):for j in range(1, len(compare_name) + 1):if input_name[i - 1] == compare_name[j - 1]:LCS[i][j] = LCS[i-1][j-1] + 1# 매칭된 '연속적인' 문자열의 길이를 체크(가장 큰 값을 넣어줌)if ans < LCS[i][j]:ans = LCS[i][j]pos = j - 1 # 제일 긴 위치의 position을 구함print("- {}와 {}\n 매칭 길이 = {}".format(compare_name, input_name, ans))# 매칭된 문자 출력str = ''if pos >= 0:for i in range(ans-1, -1, -1):str += compare_name[pos-i]str = "".join(str)print(" 매칭된 문자열 : {}\n".format(str))if __name__ == "__main__":name_list = ['jay', 'ferrnanodo', 'jake', 'jejaje', 'jqqqaeeeyy']input = 'jayji'# Longest Common Substringlcs_substring(name_list, input)
코드를 보시면 점화식 대로 비교 문자가 같을 경우 이전 값 + 1 하여 저장 하고 있습니다.(동적계획법) i,j에 -1 한 이유는 비교를 편하게 하기 위해 LCS 2차원 배열에 0번쨰 빈 칸들을 추가 했기 때문입니다.(LCS배열은 1부터 비교, input_name, compare_name은 0번째 index 부터 비교)
추가로 매칭된 문자열을 출력하는 코드도 만들어 봤습니다. 매칭 문자열을 구하는건 정말 쉽습니다. 위의 그림에서 보면 연속적이 이어야 하기 떄문에 대각선으로 값이 증가하는 규칙을 볼 수 있습니다. 그래서 저는 가장 큰 위치의 position을 구한뒤 해당 position에서 compare_name의 위치에서 -1씩 해주며 매칭된 문자열을 구하였습니다.
2. Logest Common Susequence
이번에는 원래 다루기로 했던 주제인 최장 공통 부분 수열에 대해 알아보겠습니다. 먼저 최장 공통 부분수열의 정의는
주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제다.
라고 위키에 나와 있네요! 위에서 다뤘던 최장 공통 부분 문자열과는 다르게 연속적이지 않아도 됩니다. 그림과 점화식으로 먼저 확인해 보겠습니다. 이번에도 우린 최장 공통 부분 수열의 길이를 구할것입니다.
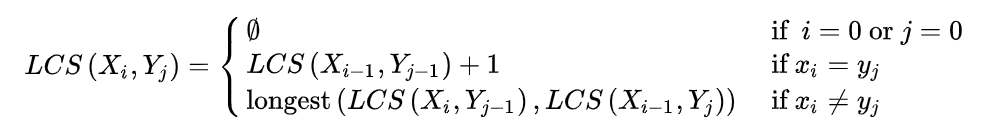
* 최장공통부분수열(위키) : https://ko.wikipedia.org/wiki/%EC%B5%9C%EC%9E%A5_%EA%B3%B5%ED%86%B5_%EB%B6%80%EB%B6%84_%EC%88%98%EC%97%B4
최장 공통 부분 수열 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 최장 공통 부분수열 문제는 LCS라고도 불린다. 이는 주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제다.(종종 단 두 개중 하나가 되기도 한다.) 컴퓨터 과학에서 고전으로 통하는 문제이며, diff 유틸리티의 근간이 되며, 생물정보학에서도 많이 응용되고 있다. 이 문제는 연속되어 있는 공통 문자열을 찾는 최장 공통 부분문자열(longest common substring) 문제와 혼동해서
ko.wikipedia.org
점화식을 두번째 조건을 보면 Xi, Yj 가 같을 경우 이전의 LCS 값 + 1 을 하게 됩니다. DP의 특징인데, 현재값을 구하기 위해 이전 범위의 값을 이용하는 것 입니다. 최장 공통 부분 수열 의 경우 연속적이 않아도 되기 때문에 이전 길이를 보존해야합니다.
그렇기 때문에 이전 값에 + 1을 해서 증가하는 것 입니다. 세번째 조건의 경우 앞의 예와 동일하게 이전의 값을 그대로 가지고 있어야 하므로, LCS값 두개 를 비교하여 더 큰 값을 가져와 유지하게 되는 것 입니다. 코드로 한번 확인해 보겠습니다!
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647def lcs_subsequence(n_list, input_name):for compare_name in n_list:LCS = [[0]*(len(compare_name)+1) for i in range(len(input_name)+1)]ans = 0for i in range(1, len(input_name) + 1):for j in range(1, len(compare_name) + 1):if input_name[i - 1] == compare_name[j - 1]:LCS[i][j] = LCS[i-1][j-1] + 1else:LCS[i][j] = max([LCS[i][j-1], LCS[i-1][j]])print("- {}와 {}\n 매칭 길이 = {}".format(compare_name, input_name, LCS[len(input_name)][len(compare_name)]))i = len(input_name)j = len(compare_name)matched_str = ""# 매칭되는 글자 출력while i != 0 and j != 0:if LCS[i - 1][j] < LCS[i][j] and LCS[i][j - 1] < LCS[i][j]:matched_str += input_name[i-1]i -= 1j -= 1elif LCS[i - 1][j] < LCS[i][j]:j -= 1elif LCS[i][j - 1] < LCS[i][j]:i -= 1else: # 같은 경우i -= 1j -= 1matched_str = "".join(reversed(matched_str))print(" 매칭 문자열 : {}\n".format(matched_str))if __name__ == "__main__":name_list = ['jay', 'ferrnanodo', 'jake', 'jejajeji', 'jqqqaeeeyyji']input = 'jayji'# Longest Common Substring#lcs_substring(name_list, input)#print('\n\n\n')# Longest Common Subsequencelcs_subsequence(name_list, input)
코드를 보시면 점화식과 동일하게 작성 된 걸 볼 수 있습니다. 알고리즘을 잘 풀기 위해서는 점화식을 잘 구해내는게 제일 중요한 것 같습니다. (저도 잘 못해서 .. 너무 알고리즘을 외우듯이 공부하는건 잘 못된 공부 방법인 것 같아요 ㅎㅎ(경험))
매칭된 문자열을 찾는 방법은 최장 공통 문자열 과 비슷합니다. 위키에 보면 역추적 접근 이라고 나오는데,
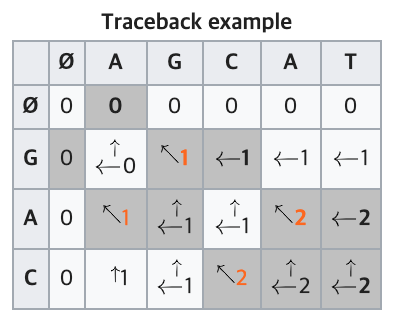
위 그림을 참고하여 코드를 보시면 쉽게 이해가 가실거에요!
오늘 말씀드릴 내용은 여기 까지 입니다. 문자열 매칭이라는게 뭔가 쉬워 보이지만, 사실 이런 알고리즘이 있다는 것 도 최근에 회사에서 슬랙봇 코드를 보면서 알게 되었네요 ㅎㅎ 앞으로는 좀 더 우리 실생활에서 쓰이는, 오래되고 검증된 알고리즘에 대해서 공부해 보려고 합니다.ㅎㅎ 다들 즐거운 코딩하세요~:D
'💻 프로그래밍 > 알고리즘' 카테고리의 다른 글
2019 카카오 1차 코딩테스트 문제 3 (자물쇠와 열쇠) (2) 2019.11.10 2019 카카오 1차 코딩테스트 문제 1 (문자열 압축) (0) 2019.11.10 [python]백준 알고리즘 11403 경로찾기 (0) 2018.01.07 카카오 1차 온라인 코딩테스트 7번 문제(17.09.16) (1) 2017.10.20 카카오 1차 온라인 코딩테스트 6번 문제(17.09.16) (6) 2017.10.16